Understand the measurements

I'm sort of a cycling nut. The events of the last week, and the last couple of years, inspired me to put down these critical thoughts on anti-doping hysteria:

Bayesian Analysis for Dummies
My training is in geophysics. I have no expertise in biology. But as a geophysicist, I have worked with measurements a lot, and I know how to assess them.

Here's a simple example. Suppose a dangerous disease affects one of every 100,000 people. A lab develops a test that is always positive if you have the disease, but that gives a false positive in one percent of cases. Your test returned positive... do you have the disease?

Well, you might. But chances are, you don't. In fact, your chances of having the disease are about one in a thousand. The “prior probability” of 100,000 to 1 dominates the test result. The test would have to show far fewer false positives to be a useful tool in diagnosing the disease.

Recent accusations against cyclists – notably Floyd Landis, Lance Armstrong, and Tyler Hamilton, have been based on biological measurements. The measurements are valuable and largely trustworthy. But the meanings of all measurements need to be assessed in light of errors and uncertainties surrounding them. A newspaper publishes an article that Landis's testosterone to epitestosterone ratio (T/E) exceed the allowed limits of 4. Let's examine the measurements.

First, go back to my earlier example. Substitute “testosterone abuse” for “deadly disease”, and assume one out of every ten cyclists is an abuser. Is Landis guilty? Probably... but not certainly: His probability of guilt would be less than 92%. So eight times out of a hundred we would be wrong to take away his victory.

But wait: the T/E test doesn't always give a positive result for abusers. Lots of abusers can pass that test. If we think 50% of abusers can scrape past, does that affect Landis's odds? Yep – now he's only 85% likely to have abused. Still want to apply a two year exile from the sport?

Here's the article that details that argument: Inferences about Testosterone Abuse among Athletes. They make this point: “Conclusions about the likelihood of testosterone doping require consideration of three components: specificity and sensitivity of the testing procedure, and the prior probability of use. As regards the T/E ratio, anti-doping officials consider only specificity. The result is a flawed process of inference.” In other words, the WADA procedures assume the test catches all abusers, and don't account for the known prevalence of abuse, so they're wrong.

Landis's Eleven
Now how about those lab results, anyway? So far, we've just accepted the lab's numbers as golden. I have heard a ratio of 11:1 for Landis. But all measurements are uncertain. How certain is that 11:1? We want error bars around that number, 11. Is there some non-zero chance the ratio is 10? 15? Even 4? If you ask WADA, it is just: Eleven. (As if Dick Pound would understand the question, or even hear you out.)

How tall are you? Can you tell me to the 32nd of an inch, or to the millimeter? How about to the nanometer? At some level of granularity, you just can no longer resolve a difference in distance. And how about that yard stick you used to measure? Pretty sure it's accurate to a millimeter? So instrument resolution is one source of uncertainty.

Uncertainty is OK! We just have to know how large the potential errors are.

In the case of the T/E ratio test, there are a lot of systems involved. Gas chromatography is well understood, and there are uncertainty estimates available for the systems they use at LNDD (Laboratoire National de Dépistage du Dopage, the Lab testing Landis's samples). The process is temperature sensitive, so we'd really want to know the uncertainty bounds on the actual temperature program they used. The instrument documentation might give us some idea how to translate temperature variations into variations at the mass spectrometer output. There might also be some pressure control program pushing material through the column; how accurately do we understand the effect of uncertainty in the pressure? The mass spectrometer itself, only a subsystem of the whole, has its own uncertainty analysis.

Below is an example of the mass spectrometer output for a similar experiment, taken from a recent paper on screening for steroids. If these peaks were epitestosterone and testosterone, this would be a picture similar to the analysis of Landis's sample.



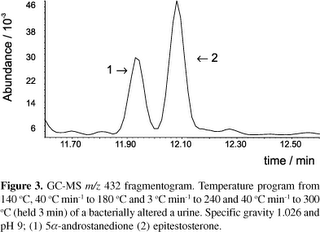
I think they get the E/T ratio by calculating the area under each of the two peaks, and dividing one by the other. So first of all, any uncertainty in the temperature and pressure would affect these areas. Secondly, the process has to separate the peaks far enough apart so that the two “hills” don't bleed into one another. Thirdly, somebody has to decide where the hills “start and stop”. See that little bump at 12.30 above? Is it part of hill 2 or not? Judgment call.

So if we know how variations in the temperature and pressure affects the shape of the picture above, and if we can estimate how the uncertainty in the temperature and pressure during this test on Landis's sample, then we'd have some decent error bars on Landis's “Eleven”.

Once you have error bounds on Landis's T/E ratio, you revisit the Bayesian analysis. Any appreciable uncertainty will decrease the likelihood that Landis abused testosterone.

The analysis of Landis's sample won't stop with the T/E ratio test, of course. The next step evidently may be an IRMS analysis for the ratios of two carbon isotopes. As the news emerges, you should ask how the test works, and what are the uncertainties.

Armstrong and Hamilton
And so with the charges against Armstrong made by l'Equipe last year, and with those against Tyler Hamilton in 2004. In Armstrong's case, the uncertainty begins with the chain of custody. Then you have an experimental test, applied to six year old samples. In the Hamilton case, the anti-doping agencies placed full faith and credit in a new test – only published months earlier -- with documented repeatability problems. The actual procedures in executing these tests are more complex and sensitive than the procedures for T/E. Yet, all we get from the lab is, “positive”. These positives are the results of judgments, made in good faith presumably, but not subject to review by the athletes or the public (see e.g. the Vrijman report).

My point isn't that these men are innocent. My point is that the probability of their guilt is far less than the public assumes from news reports. We can pardon the public, and even the press, for putting more faith in the numbers than they deserve. But the bureaucrats at the anti-doping agencies irresponsibly accuse athletes. They pay lip service to “science” but know nothing of it. They make great displays to be the most earnest of witch burners, lest they endanger their jobs for lack of vigor pursuing dopers. Cycling pays the price.

Additional Reading
Can we handle the truth? We are our own worst enemy -- Knowledgeably explores the madness and injustice of the anti-doping regimes, from someone inside the sport.